Zum Navigationspfad Unterseiten von „Forschung und Projekte“ Zur Navigation Zum Schnellzugriff Zum Fuß der Seite mit weiteren Services
Zum Inhalt
Fakultät Maschinenbau
Studenten im Sommer auf dem Campus Nord, rote Zahnräder im Hintergrund © Roland Baege​/​TU Dortmund

Gruppe Mathematische Optimierung

Hier finden Sie Informationen zu den einzelnen Themen-Schwerpunkten der Mathematischen Optimierung.

Darstellung eines Hofplans mit LKW an Toren im Vordergrund und ein Ablaufplan im Hintergrund © ITL​/​TU Dortmund
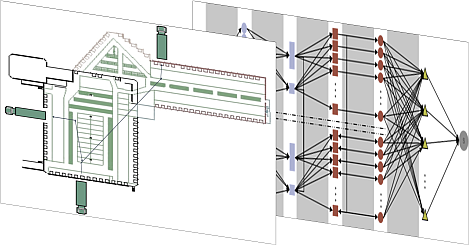
  • Optimale Torbelegungen in logistischen Anlagen (z.B. für Stückgutspeditionen)
  • Minimierung der Betriebskosten für innerbetriebliche Hauptprozesse (Entladung, Verbringung und Beladung)
  • Zeitgenaue Zuweisung von Touren und Relationen zu Eingangs- und Ausgangstoren
  • Modelle & Algorithmen:
    • Mehrgüterflussmodelle mit Zeitscheiben
    • Column Generation Algorithmen
    • Scheduling-Heuristiken
Darstellung eines abstrakten Netzes im Vordergrund und mathematische Modell im Hintergrund © ITL​/​TU Dortmund
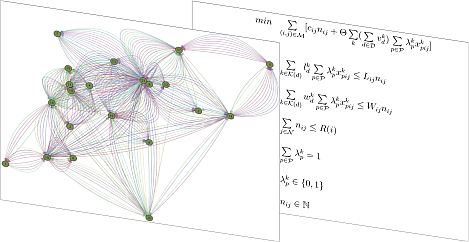
  • Effiziente Bündelung und Routing von Transportflüssen in Netzen des Schienengüterverkehrs und Straßengüterverkehrs
  • Optimierung auf Basis gegebener Netzstrukturen (Kunden, Standorte, Hubs)
  • Kopplung an eine strategische Netzplanung
  • Abbildung realer Transportkosten (z.B. auf Basis von LKW, Zügen) und Umschlagkosten in den logistischen Knoten
  • Modelle & Algorithmen:
    • Mehrgüterflussmodelle
    • Network Design Modelle
    • Column Generation Verfahren
    • Branch-and-Price-and-Cut Verfahren
    • Matheuristics
Grafische Darstellung einer Dienstplanung © ITL​/​TU Dortmund
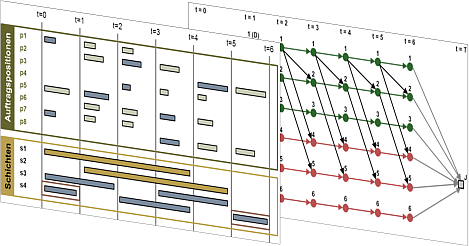
  • Personalbedarfsplanung und Personaleinsatzplanung in logistischen Anlagen (z.B. Distributionszentren)
  • Robuste integrierte Umlauf- und Dienstplanung im öffentlichen Verkehr
  • Dienstplanung und Personaleinsatzplanung in den Bereichen Transport, Verkehr und Entsorgung
  • Integration harter und weicher Aspekte in die Planung (z.B. Kosten, Mitarbeiterzufriedenheit, rechtliche und betriebliche Regeln & Restriktionen)
  • Kopplung mit der Planung oder Steuerung logistischer Ressourcen (z.B. Stapler, Transportfahrzeuge, Umläufe)
  • Modelle & Algorithmen:
    • Set Partitioning & Set Covering Modelle mit zusätzlichen Nebenbedingungen
    • Column Generation Algorithmen
    • Lagrange Relaxation und Subgradienten-Optimierung
    • Ressource Constrained Shortest Path Algorithmen
abstrakte Darstellung eines Transportnetzes im Vordergrund und Darstellung der Quelle-Senke-Beziehung im Netz zwischen allen Punkten im Hintergrund © ITL​/​TU Dortmund
  • Optimierung von vorhandenen Netzstrukturen im Schienengüterverkehr und Straßengüterverkehr
  • Neuplanung von Netzstrukturen und Standorten im Schienengüterverkehr und Straßengüterverkehr
  • Mehrstufige Netzplanung mit Berücksichtigung unterschiedlicher Standorttypen, -funktionen und -kapazitäten
  • Abbildung realer Transportkosten (z.B. auf Basis von LKW oder Zügen) sowie Umschlagkosten in den logistischen Knoten
  • Modelle & Algorithmen:
    • (gemischt) ganzzahlige Network Design und Flussmodelle
    • Multi-Allocation-Modelle (individuelles Routing jeder Sendungsrelation) mit realen Transportkosten auf Basis der eingesetzten Fahrzeuge
    • Branch & Bound, Branch & Cut sowie Column Generation Algorithmen
    • Problemspezifische Heuristiken
Landkarte von Nordrhein-Westfalen im Vordergrund und Darstellung einer Routenplanung im Hintergrund © ITL​/​TU Dortmund
  • Robuste Sammelgut-Nahverkehrstourenplanung als Pickup-And-Delivery Problemstellungen
  • Abbildung stochastischer Einflüsse wie Fahrzeiten und Kundenbedarfe
  • Minimierung benötigter Fahrzeuge sowie Minimierung von Fahrtkosten und Ankunftszeiten
  • Szenariengenerierung zur Abbildung der stochastischen Einflüsse
  • Strategische Gebietstourenplanung auf Basis von Ist-Soll-Szenarien
  • Modelle & Algorithmen:
    • Zweistufiges stochastische Optimierungsmodelle
    • Savings-Verfahren
    • k-opt Operatoren
    • Scenario Decomposition
    • Evolutionäre Algorithmen
abstraktes Netz mit Knoten und Kanten dahinter ein Ablaufplan © ITL​/​TU Dortmund
  • (gemischt) ganzzahlige Mehrgüterflussmodelle mit Zeitscheiben
  • (gemischt) ganzzahlige Network Design Modelle
  • Multi-Allocation-Modelle (individuelles Routing jeder Sendungsrelation) mit realen Transportkosten auf Basis der eingesetzten Fahrzeuge
  • Zweistufige stochastische Optimierungsmodelle
  • Set Partitioning & Set Covering Modelle mit zusätzlichen Nebenbedingungen
  • Lagrange Relaxation und Subgradienten-Optimierung
  • Column Generation Verfahren
  • Ressource Constrained Shortest Path Algorithmen
  • Branch-and-Price-and-Cut Verfahren
  • Evolutionäre Algorithmen
  • Problemspezifische Heuristiken / Matheuristics
  • Savings-Verfahren & k-opt Operatoren
  • Scenario Decomposition

Ansprechperson: Nele Pommerening, M.Sc.

Ausgewählte Projekte der Gruppe Mathematische Optimierung

Gesamtübersicht

Zum Seitenanfang